System.Numerics.Vector is a library provided by .NET (as a NuGet package) that exposes value types such as Vector<T> which are recognized by RyuJIT as intrinsics. Supported intrinsics are listed in the coreclr repository. This enables C# SIMD acceleration, as long as you modify your code to use these intrinsic types instead of scalar floating point elements.
On the other hand, Hybridizer aims to provide these benefits without being intrusive in the code (only metadata is required).
We naturally wanted to test if System.Numerics.Vector delivers good performance, compared to Hybridizer.
Summary
We measured that Numerics.Vector provides good speed-up over C# code as long as no transcendental function is involved (such as Math.Exp), but still lags behind Hybridizer. Because of the lack of some operators and mathematical functions, Numerics can also generate really slow code (when the AVX pipeline is broken). In addition, code modification is a heavy process, and can’t easily be rolled back.
We wrote and ran two benchmarks, and for each of them we have four versions:
- Simple C# scalar code
- Numerics.Vector
- Simple C# scalar code, hybridized
- Numerics.Vector, hybridized
Processor is a Core i7-4770S @ 3.1GHz (max measured turbo in AVX mode being 3.5GHz). Peak flops is 224 GFlop/s, or 112 GCFlop/s if we count FMA as one (supported on this processor).
Compute bound benchmark
This is a compute‑intensive benchmark. For each element of a large double‑precision array (8 million elements: 67 MB), we iterate twelve times the computation of an exponential’s Taylor expansion (expm1). This is largely enough to enter the compute‑bound world by hiding memory latencies behind a full bunch of floating‑point operations.
Scalar code is simply:
[MethodImpl(MethodImplOptions.AggressiveInlining)]public static double expm1(double x){ return ((((((((((((((15.0 + x) * x + 210.0) * x + 2730.0) * x + 32760.0) * x + 360360.0) * x + 3603600.0) * x + 32432400.0) * x + 259459200.0) * x + 1816214400.0) * x + 10897286400.0) * x + 54486432000.0) * x + 217945728000.0) * x + 653837184000.0) * x + 1307674368000.0) * x * 7.6471637318198164759011319857881e-13;}
[MethodImpl(MethodImplOptions.AggressiveInlining)]public static double twelve(double x){ return expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(expm1(x)))))))))));}We added the AggressiveInlining attribute to help RyuJIT merge operations at JIT time.
The Numerics.Vector version of the code is quite the same:
[MethodImpl(MethodImplOptions.AggressiveInlining)]public static Vector<double> expm1(Vector<double> x){ return ((((((((((((((new Vector<double>(15.0) + x) * x + new Vector<double>(210.0)) * x + new Vector<double>(2730.0)) * x + new Vector<double>(32760.0)) * x + new Vector<double>(360360.0)) * x + new Vector<double>(3603600.0)) * x + new Vector<double>(32432400.0)) * x + new Vector<double>(259459200.0)) * x + new Vector<double>(1816214400.0)) * x + new Vector<double>(10897286400.0)) * x + new Vector<double>(54486432000.0)) * x + new Vector<double>(217945728000.0)) * x + new Vector<double>(653837184000.0)) * x + new Vector<double>(1307674368000.0)) * x * new Vector<double>(7.6471637318198164759011319857881e-13);}The four versions of this code give the following performance results:
| Flavor | Scalar C# | Vector C# | Vector Hyb | Scalar Hyb |
|---|---|---|---|---|
| GCFlop/s | 4.31 | 19.95 | 41.29 | 59.65 |
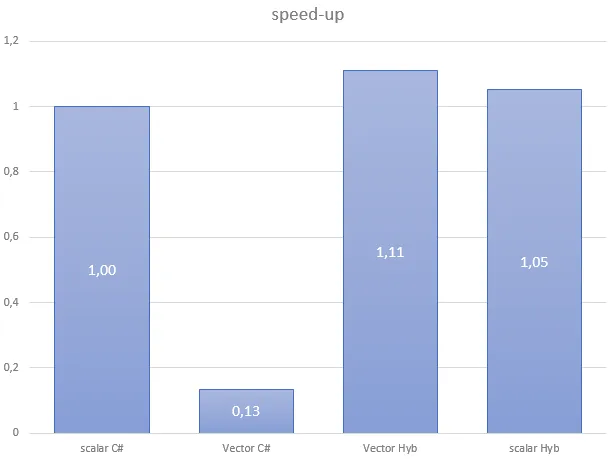
As stated, Numerics.Vector delivers a close to 4× speedup over scalar. However, performance is far from what we reach with Hybridizer. If we look at generated assembly, it’s quite clear why:
vbroadcastsd ymm0,mmword ptr [7FF7C2255B48h]vbroadcastsd ymm1,mmword ptr [7FF7C2255B50h]vbroadcastsd ymm2,mmword ptr [7FF7C2255B58h]vbroadcastsd ymm3,mmword ptr [7FF7C2255B60h]vbroadcastsd ymm4,mmword ptr [7FF7C2255B68h]vbroadcastsd ymm5,mmword ptr [7FF7C2255B70h]vbroadcastsd ymm7,mmword ptr [7FF7C2255B78h]vbroadcastsd ymm8,mmword ptr [7FF7C2255B80h]vaddpd ymm0,ymm0,ymm6vmulpd ymm0,ymm0,ymm6vaddpd ymm0,ymm0,ymm1vmulpd ymm0,ymm0,ymm6vaddpd ymm0,ymm0,ymm2vmulpd ymm0,ymm0,ymm6vaddpd ymm0,ymm0,ymm3vmulpd ymm0,ymm0,ymm6vaddpd ymm0,ymm0,ymm4vmulpd ymm0,ymm0,ymm6vaddpd ymm0,ymm0,ymm5vmulpd ymm0,ymm0,ymm6vaddpd ymm0,ymm0,ymm7vmulpd ymm0,ymm0,ymm6vaddpd ymm0,ymm0,ymm8vmulpd ymm0,ymm0,ymm6; repeatedFused multiply-add are not reconstructed, and constant operands are reloaded from the constant pool at each expm1 invocation. This leads to high register pressure (for constants), where memory operands could save some.
Here is what Hybridizer generates from scalar code:
vaddpd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vfmadd213pd ymm1,ymm0,ymmword ptr []vmulpd ymm0,ymm0,ymm1vmulpd ymm0,ymm0,ymmword ptr []vmovapd ymmword ptr [rsp+0A20h],ymm0; repeatedThis reconstructs fused multiply-add and leverages memory operands to save registers.
Why are we not at peak performance (112 GCFlops)? Haswell has two pipelines for FMA and a latency of 5. To reach peak performance, we would need to interleave two independent FMA instructions each cycle. This could be done by reordering instructions, but the backend compiler is not capable of such reordering. To get better performance, we would have to write assembly by hand.
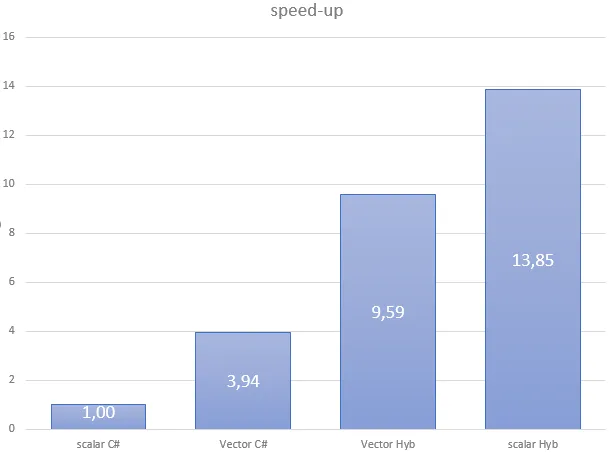
Invoke transcendentals
In this second benchmark, we need to compute the exponential of all the components of a vector. To do that, we invoke Math.Exp.
Scalar code is:
[EntryPoint]public static void Apply_scal(double[] d, double[] a, double[] b, double[] c, int start, int stop){ int sstart = start + threadIdx.x + blockDim.x * blockIdx.x; int step = blockDim.x * gridDim.x; for (int i = sstart; i < stop; i += step) { d[i] = a[i] * Math.Exp(b[i]) * Math.Exp(c[i]); }}In this context, Numerics.Vector cannot directly call vectorized transcendentals, so code often falls back to scalar loops or repeated calls that break the AVX pipeline. Hybridizer, however, can generate efficient vectorized code for the same logic.